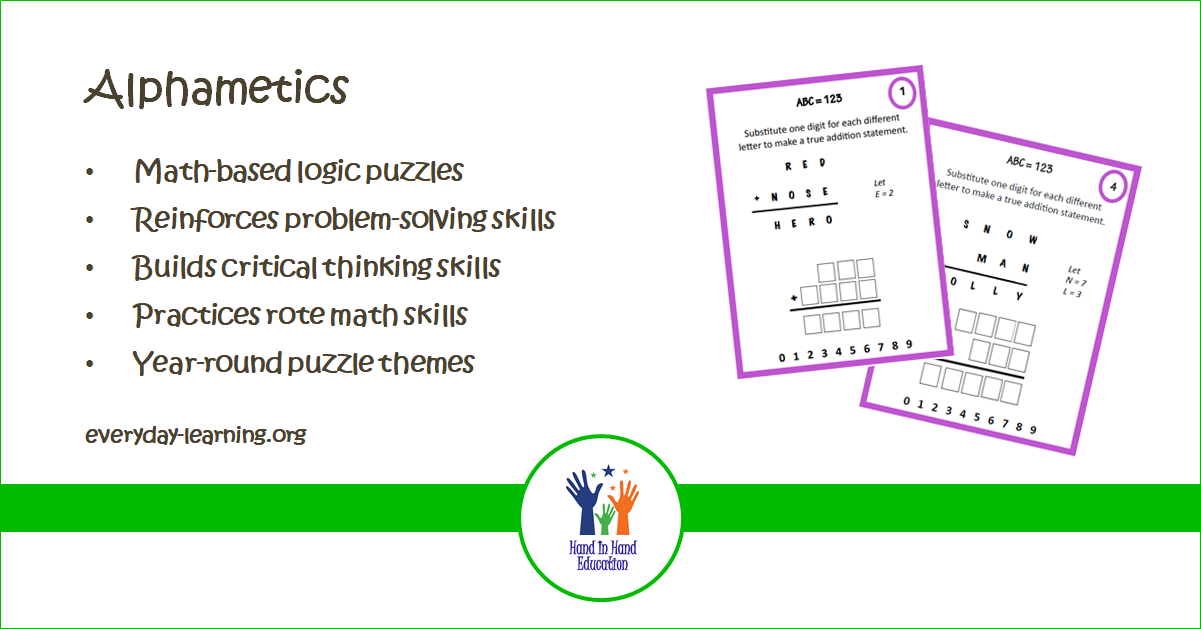
Alphametic Problem Solving Strategies
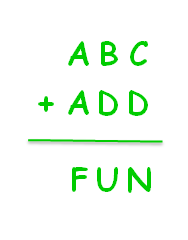
Alphametics are a type of verbal arithmetic brainteaser. They look easy to solve, but they can prove to be a real head scratcher if you just take a trial-and-error approach.
Basic Rules for Solving Alphametics
- Each letter represents a different single digit
- If a letter is used more than once, it represents the same digit
- Your letter-digit substitutions must make a true math problem
- An alphametic can have more than one correct answer
Before you start solving an alphametic brainteaser with your students, it will be helpful to review the Additive Identity and the Commutative Properties of Addition.
Challenge students to think about how these math properties might show up in an alphametic puzzle.
For example, the Additive Property – the rule that any number plus zero always equals itself – would look like this alphametic:
A + B = A
(This looks a lot like an algebraic equation. Sneaky, I know. But alphametics focus on developing thoughtful approaches to problem solving, where students move from blindly Guessing and Checking to Finding Patterns, Making Lists, and Using Logical Reasoning.)
In this example, students can quickly deduce that:
B = 0
On the other hand, A can equal any digit from 1 to 9. So, 1 + 0 = 1 would be a true answer for this alphametic puzzle, but so would 2 + 0 = 2 and 3 + 0 = 3 and so on.
Easy, right? Now, let’s see what happens when you have 2 or more columns in an alphametic brainteaser.

Once kids can identify that a single group of ten is being carried from the ONES column, they have identified a clue in solving this alphametic problem.
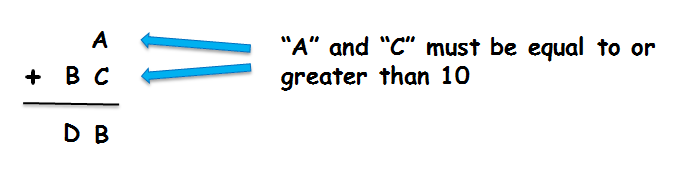
This is a good place to stop and list everything you know about your alphametic problem:
- B + 1 = D
- B cannot equal 0 or 9
- A + C >= 10
- A + C <= 17
Why? The only two single digits that equal 18 are 9 and 9. Since A and C must be different digits, the ONES Column sum cannot be 18.
Now that you know some clues we are almost ready to plug numbers in to see what might satisfy this equation.
Start by brainstorming any set of facts that equal 10, 11, 12, … 17.
If we randomly choose A = 7 and C = 5, we see:
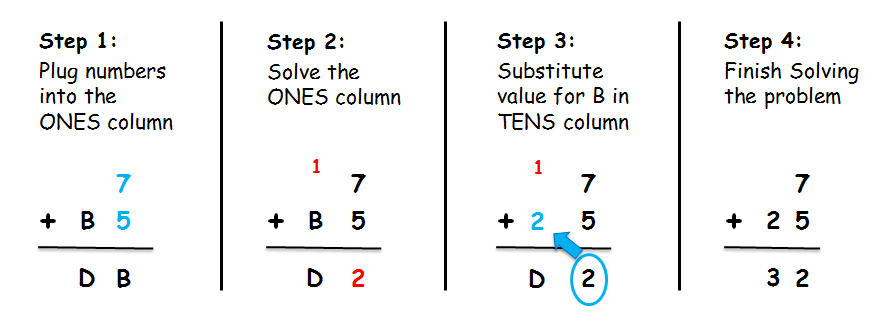
SUCCESS! But here’s the fun news: We could have chosen different values for A and C and still gotten a correct solution. This particular problem has 18 different answers that work.
Let’s take a look at a harder alphametic problem:
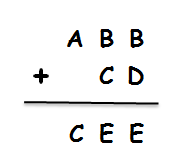
Before we start trying to solve this problem, take a look at ONES and TENS columns.

Since each letter must be represented by a different digit, the only way both of these statements can be true is if we carry a group of tens into the TENS Column. Knowing that means we can deduce:
C + 1 = D
Next, we look at the HUNDREDS Column. We already know that any number plus zero must equal itself. So, the only way A = C is if we carry over to this column, also. We now have a second rule we must remember:
A + 1 = C
At this point, we have enough information to make an educated guess on how to solve this puzzle. We can begin by randomly choosing A=1, C=2, and D=3.

If we substituted B = 8, the ONES Column would equal 11. We know that E cannot be 1, 2, or 3 because those digits were used for A, C, and D. A similar problem happens if we try B = 9. So, in this scenario, the only possible answer is for B to equal 7.
Can you solve this alphametic when you start with A = 2?
Alphametics can be used with math whiz kids who enjoy solving logic problems, as well as with kids struggling to master basic addition facts. The key to happy success is modeling thoughtful problem solving approaches.
Other Hints for Having Fun with Alphametics
- Use a white board
- Color code letters in a puzzle
- Use a number chart and erase digits once they’ve been used in a puzzle
- Walk students through the process of looking for problem solving clues at least 3 times before having them try a problem on their own
- Jumpstart a solution by providing a single letter answer
- Have a sense of humor
- Remember, many alphametics have more than one answer
Do you enjoy building math resilience with these kinds of brainteasers? Get more Alphametic Puzzles for your kids to work on.